[PHẦN 1] Tính Toán Thiết Kế Và Kích Thước Của Lò Xo Lá Dạng Parabol

Tính toán thiết kế và kích thước của lò xo lá- nhíp lá dạng parabol đang là một trong những chủ đề rất được quan tâm. Đây được xem là bước cơ bản những rât quan trọng, đặc biệt là trong các lĩnh vực chế tạo máy, ô tô,… Bài viết hôm này sẽ giúp anh em hiểu rõ hơn quy trình này. Xem ngay nhé!

Các điều kiện tải trọng sau đây có ảnh hưởng đáng kể nhất định đến tính nhất quán của lò xo lá- nhíp lá trục trước:

• Tải trọng dọc thuần túy xuất hiện trong quá trình lái xe trên đường thẳng.
• Tải trọng dọc xảy ra do việc phanh.
• Giá trị lớn nhất của hai điều kiện tải trọng trên được biểu thị theo mối quan hệ nửa trọng tải của xe F (n). Chúng được tính đến để thiết kế chính xác độ bền của sản phẩm cuối cùng.

Bảng 1. Tải trọng và các thông số hình học của lò xo lá

Tải trọng dọc tối đa F (v,max) trong quá trình lái xe trên đường thẳng được xác định bởi:

Lực dọc và tải trọng dọc cực đại F_(v,max) và F_(br,max) khi tác động hết hành trình bàn đạp phanh được tính toán như sau:

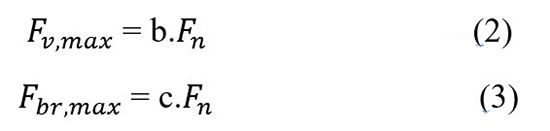
Ứng suất do tải trọng dọc lớn nhất và do phanh đều được tính đến trong thiết kế. Các thông số thiết kế và kích thước của lò xo lá- nhíp lá dạng parabol được cho trong bảng 1

Phân tích lá lò xo dạng parabol bằng phương pháp phần tử hữu hạn

Ứng suất và độ chuyển vị lớn nhất trên lò xo lá- nhíp lá dạng parabol ba lớp được tính bằng công thức (4) và (5):

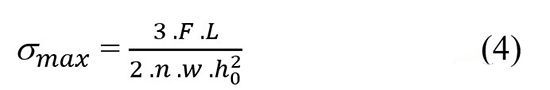
Kết quả ứng suất và chuyển vị lớn nhất đối với tải trọng thiết kế và tải trọng lớn nhất được thể hiện trong Bảng 2.

Bảng 2. Ứng suất và chuyển vị lớn n

Biểu đồ tải trọng lý thuyết và độ dịch chuyển của lò xo lá- nhíp lá dạng parabol được biểu diễn trên hình 4.

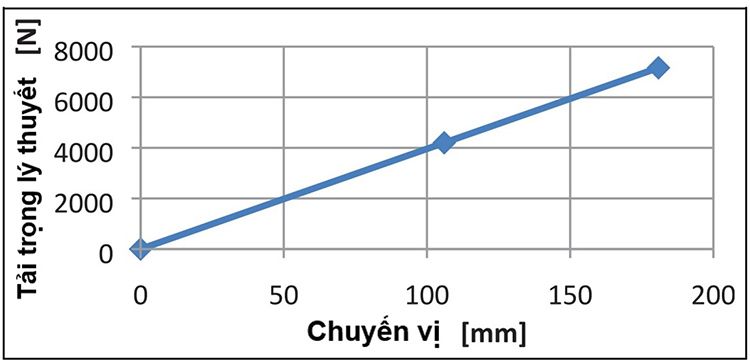
Hình 4. Biểu đồ tải trọng và chuyển vị lý thuyết

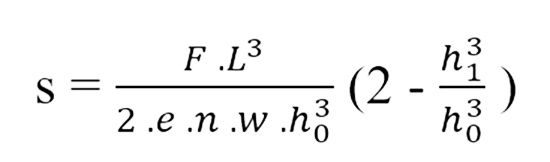
Trong đó :

σ (max) là ứng suất lớn nhất trên lò xo (MPa),

s là độ võng của lá lò xo (mm),

F là lực (N),

n là số lớp của lò xo,

w là chiều rộng của lò xo (mm),

h (0) là độ dày ở tâm (mm),

h (1) là độ dày ở đầu cố định (mm),

L là chiều dài của lò xo (mm)

E là môđun đàn hồi của vật liệu làm lò xo.

Độ cứng của lá lò xo dạng parabol k được tính ra 39,6 bằng cách sử dụng phương trình (6):

Thiết kế mô hình 3D với sự hỗ trợ của máy tính

Mô hình hóa thiết kế có sự hỗ trợ của máy tính (CAD) của một lò xo lá- nhíp lá dạng parabol được thực hiện bằng cách sử dụng CATIA V5 R20 trong môi trường Part Design Workbench. Bản chất là sử dụng mô hình CAD đã phát triển làm mẫu vật lý trước khi sản xuất mẫu thử nghiệm. Các vật liệu được gán cho mô hình và các đặc tính của nó lần lượt được trình bày trong Hình 5 và Bảng 3.

Phân tích phần tử hữu hạn

FEM là một phương pháp số có thể được sử dụng để tìm giải pháp cho một số vấn đề kỹ thuật liên quan đến phân tích ứng suất. ANSYS là một chương trình máy tính phần tử hữu hạn đa năng. Mô hình 3D của một lò xo lá- nhíp lá dạng parabol được tạo ra bằng cách sử dụng CATIA V5 được nạp vào ANSYS để chia lưới, điều chỉnh các điều kiện biên và quá trình phân tích.

Mô hình chia lưới

Chia lưới chỉ đơn giản là quá trình cắt một mô hình 3D thành các phần tử nhỏ để chuẩn bị cho phân tích. Mô hình lưới phần tử hữu hạn của lò xo lá- nhíp lá dạng parabol có các tính chất sau. Các đặc tính của mô hình lưới được cho trong Bảng 4. Mô hình lưới của lò xo lá- nhíp lá dạng parabol được thể hiện trong Hình 6.

Hình 5. Mô hình CAD của lò xo lá- nhíp lá dạng parabol

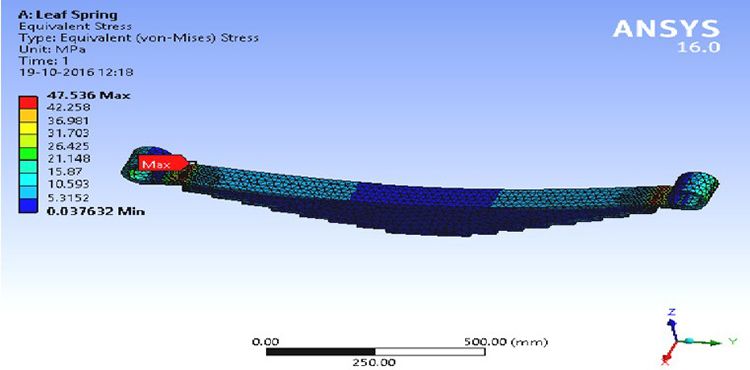
Hình 6. Mô hình chia lưới của lò xo lá- nhíp lá dạng parabol

Bảng 3. Các đặc tính của mô hình

Bảng 4. Các đặc tính của mô hình lưới

Điều kiện biên

Để mô phỏng các điều kiện thực tế của cụm chi tiết cho việc phân tích, các điều kiện biên đã được phân tích như sau:

• Mắt trước của lò xo lá- nhíp lá bị cưỡng bức tịnh tiến theo các hướng x, y và z; quay theo hướng x và z bằng cách cho phép quay tự do theo hướng y.
• Mắt sau của lá lò xo được cố định khi tịnh tiến theo phương y và z và quay theo phương x và z bằng cách cho phép tịnh tiến tự do theo phương x và quay tự do theo phương y.
• Tải trọng trục tác dụng theo phương thẳng đứng. Vật liệu của các bộ phận của lò xo lá- nhíp lá dạng parabol như đã chỉ định.

Phân tích cấu trúc tĩnh

Phân tích cấu trúc tĩnh của lò xo lá- nhíp lá dạng parabol đã được thiết lập cho tải trọng thiết kế và tải trọng lớn nhất.

Tải trọng tác dụng

Tải trọng tác dụng được xem xét theo 2 giai đoạn đối với tải trọng thiết kế và tải trọng lớn nhất như sau:

• Theo tải trọng thiết kế: Kết quả phân tích với ứng suất von-Mises là 4200 (N) và chuyển vị lớn nhất được thể hiện ở hình 7 và 8.
• Dưới tải trọng thiết kế: trong khi ứng suất lớn nhất của lò xo là 468 MPa, độ dịch chuyển của lò xo là 110 mm.
• Theo tải trọng lớn nhất: Kết quả phân tích với ứng suất von-Mises là 7163 (N) và chuyển vị lớn nhất được thể hiện ở hình 9 và 10.
• So sánh các phương pháp đối với tải trọng thiết kế và tải trọng lớn nhất được nêu ở Bảng 5. Dưới tải trọng lớn nhất, trong khi ứng suất lớn nhất của lò xo là 779 MPa, độ dịch chuyển của lò xo là 193 mm.

Phân tích sự đứt gãy do mỏi

Mô hình hư hỏng do mỏi bao gồm cơ chế nứt mỏi và mô hình dự đoán độ bền mỏi. Cơ chế nứt mỏi và các mô hình dự đoán độ bền mỏi được mô tả như sau:

* Cơ chế hiện tượng nứt do mỏi

Quá trình mỏi thường liên quan đến sự phát triển của các vết nứt vi mô và sự lan truyền vết nứt vĩ mô. Sự phát triển của vết nứt vi mô bao gồm sự khởi đầu, gia tăng và lan truyền.

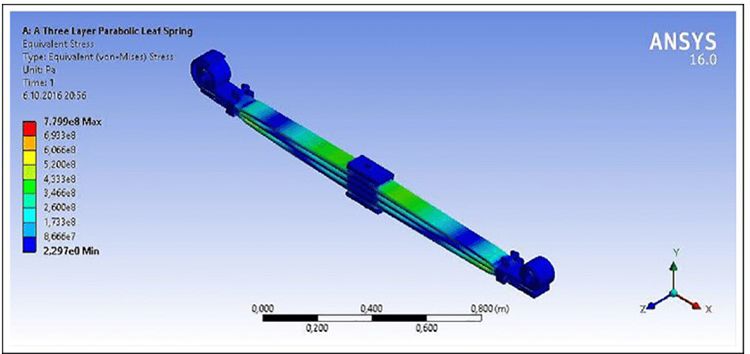
Hình 7. Phân tích ứng suất của lò xo lá- nhíp lá theo tải trọng thiết kế

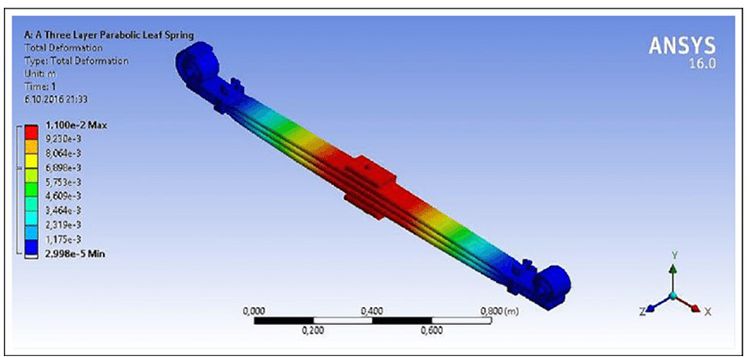
Hình 8. Phân tích biến dạng của lò xo lá- nhíp lá theo tải trọng thiết kế

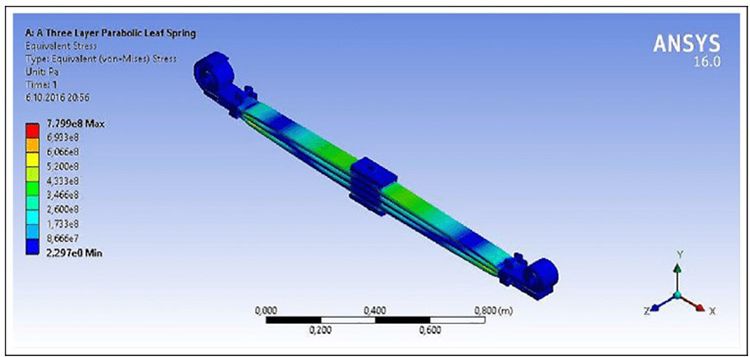
Hình 9. Phân tích ứng suất của lò xo lá- nhíp lá theo tải trọng lớn nhất

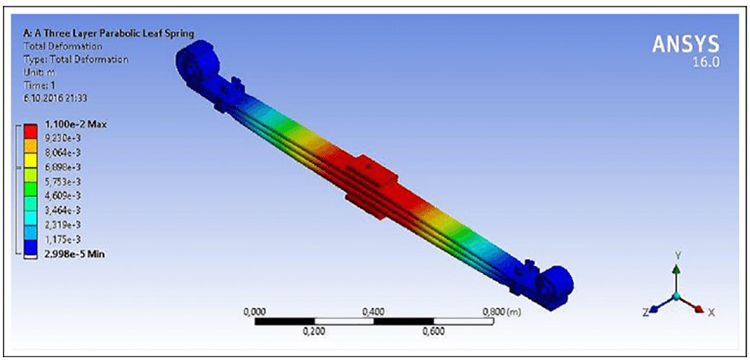
Hình 10. Phân tích biến dạng của lò xo lá- nhíp lá theo tải trọng lớn nhất

Bảng 5. So sánh các phương pháp dựa trên tải trọng thiết kế và tải trọng lớn nhất

Sự bắt đầu của các vết nứt vi mô có thể xảy ra trực tiếp tại các lỗ hổng ban đầu của vật liệu hoặc bắt đầu bằng những thay đổi cấu trúc vi mô do tải trọng gây ra theo chu kỳ dẫn đến hư hỏng vĩnh viễn và sau đó hình thành các vết nứt vi mô trong vật liệu. Các vết nứt nhỏ này gia tăng với số lượng chu kỳ tải trọng ngày càng tăng.

Cuối cùng, đứt gãy do mỏi xảy ra khi một vết nứt nhỏ duy nhất đạt đến kích thước tới hạn và sau đó lan truyền một cách không ổn định. Động lực học phát triển của các vết nứt vi mô chỉ ra rằng kích thước của vết nứt vi mô (a) tăng theo số chu kỳ tải trọng (N) và tải trọng tác dụng (∆); một cách khác, mô hình chung về tốc độ tăng trưởng da/dN như là một hàm về phạm vi ứng suất ∆K được đưa ra bởi Qian và Lei.

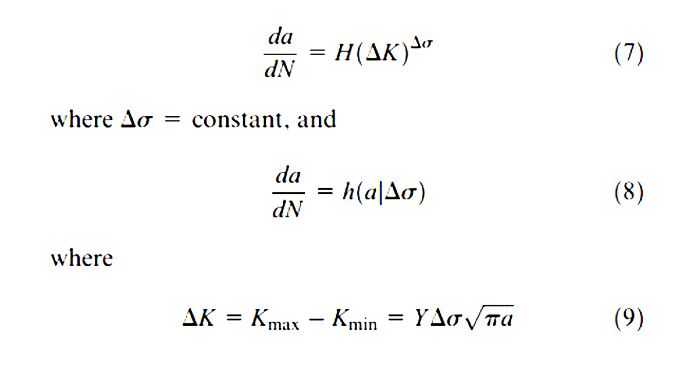
K (max) và K (min) lần lượt là hệ số cường độ ứng suất lớn nhất và nhỏ nhất.
Tiêu chuẩn của Luật Paris đối với động thái gia tăng của một vết nứt vĩ mô dưới tải trọng theo chu kỳ là một hàm lũy thừa. Nó mô tả tốc độ phát triển của một vết nứt với kích thước tức thời (a) tại chu kỳ tải trọng thứ N như một hàm lũy thừa của kích thước vết nứt.

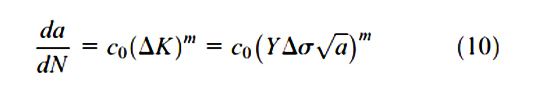
Mô hình phỏng đoán độ bền mỏi

Các mô hình phỏng đoán độ bền mỏi được phân loại là mô hình xác định hoặc mô hình xác suất (thống kê). Một số mô hình phỏng đoán độ bền mỏi được tóm tắt như sau.

Các mô hình xác định. Các mô hình xác định giữa ứng suất và độ bền đã được đề xuất theo kinh nghiệm làm tiêu chí để mô tả sự tương quan S-N đối với một mẫu vật có kích thước nhất định. Một số mô hình S-N xác định các phạm vi áp dụng ứng suất và biến dạng (∆, ∆ε) như các thông số phá hỏng do mỏi cơ bản. Một số tiêu chí xác định về phá hỏng do mỏi được trình bày dưới đây:

Tiêu chí quyết định mỏi xác định dựa trên ứng suất đã được bài viết này là giới thiệu về bởi Wöhler vào năm 1870. Theo Wöhler tiêu chí quyết định mệt mỏi được xác định như sau:

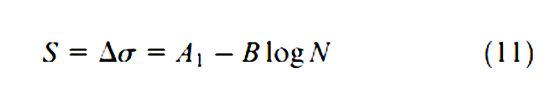
Trong đó:

• S là ứng xuất luân phiên
• N là độ bền mỏi được cho bởi số chu kỳ đứt gãy
• A1 và B là các hằng số

Vào năm 1910, Basquin đã bài viết này là giới thiệu về tiêu chí để đánh giá độ bền mỏi dựa trên ứng suất được xác định như sau:

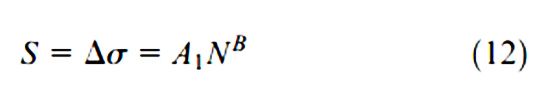
Coffin và Manson lại đưa ra tiêu chí xác định khác vào năm 1954 như sau:

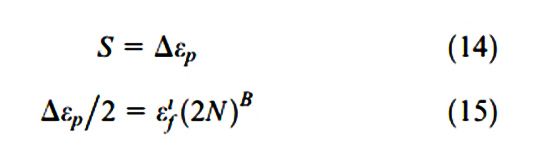
Trong đó :

• ∆ε_p/2 là biên độ biến dạng dẻo
• ε_f^1 là hệ số biến dạng dẻo do mỏi
• N là độ bền mỏi được cho bởi số chu kỳ đứt gãy
• B là hằng số.

Các mô hình xác suất

Ứng suất chính của 1 mô hình xác suất (thống kê) về độ bền mỏi được tóm lược trong 3 biến (S, N, V) và đang được xem xét. Một số mô hình xác suất P = F (S, N, V) được trình bày như sau:

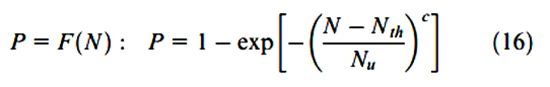
Trong đó:

N (u), N (th) và c là hàm của S = ∆σ

Vào năm 2016, Sandberg và Olsson giới thiệu về ra mô hình với độ bền mỏi theo xác suất dựa trên thể tích được xác định như sau:

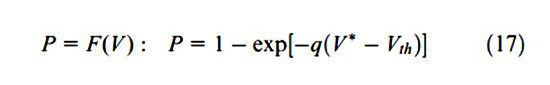
Trong đó :

V* là ứng suất theo thể tích với σ ≥ N (th ).q, V (th) và V (th ) là các thông số của vật liệu.

Castillo et al lại đưa ra nghiên cứu về khác vào năm 2009 như sau:

* Phân tích độ bền mỏi

Một số bài thử nghiệm kỹ thuật khác nhau đã có nhằm mục đích đo lường độ phản hồi của vật liệu đối với ứng suất và biến dạng theo thời gian. Thử nghiệm lâu đời nhất được trình bày bởi Wöhler vào năm 1870. Đồ thị Wöhler hoặc S-N thể hiện trong Hình 11 đã trở thành phương pháp tiêu chuẩn để mô tả đặc tính của cường độ vật liệu khi chịu tải động.

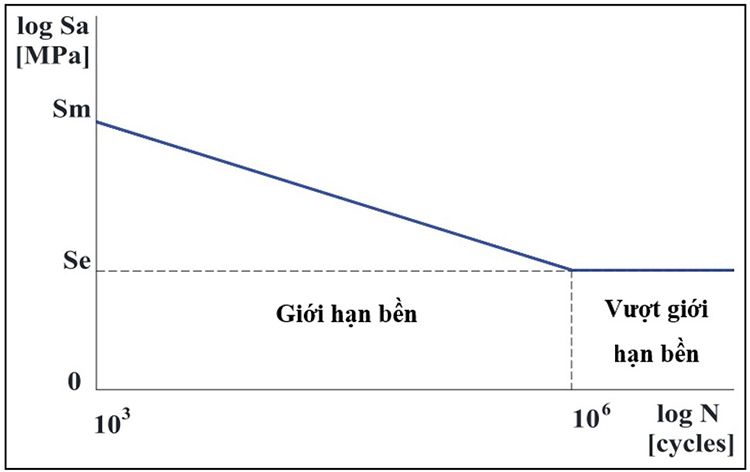
Chú ý rằng độ bền mỏi S giảm tuyến tính trên 2 trục tọa độ như 1 hàm đường thẳng và chạm đến giới hạn khi chu kỳ N bằng 10^6 hoặc 10^7.

Đây là giới hạn bền của vật liệu, vùng mà cho phép ứng suất dưới mức mà vật liệu có thể làm việc theo chu kỳ vô hạn mà không bị hỏng. Giới hạn độ bền gần đúng cho các loại thép được xác định như sau:

Cường độ mỏi hoặc giới hạn độ bền thu được từ các mẫu thử phải được sửa đổi để tính đến sự khác biệt vật lý giữa mẫu thử và bộ phận thực tế đang được thiết kế. Những khác biệt này được xem xét bằng cách sử dụng một tập hợp các yếu tố giảm cường độ được cho dưới đây:

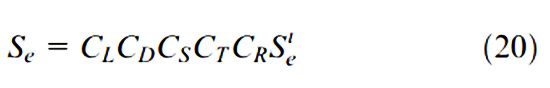
Trong đó :

• S (e) là giới hạn độ bền đã hiệu chỉnh cho vật liệu
• C (L) là hệ số giảm độ bền theo tải trọng thay đổi giữa ứng suất uốn và tải dọc trục.
• C (D) là hệ số giảm cường độ thứ nguyên và được xác định như sau :

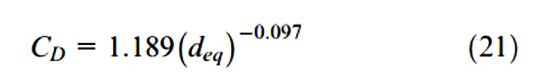
Trong đó :

d (eq) là đường kính tương đương và được tính theo công thức sau:

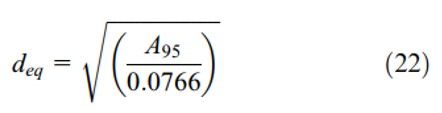
A (95) là 95% diện tích ứng suất và được tính toán dựa trên diện tích hình chữ nhật với 2 thông số b và h:

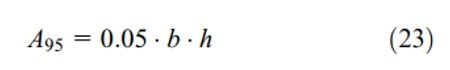
Thông số nhiệt độ C (T) được xác định theo T ≤ 450°C như C (T) = 1. Hệ số độ bền C (R) nằm trong khoảng 1 (ứng với 50% độ bền) và 0.702 (ứng với 99.99% độ bền).

Biểu đồ S-N đã đánh giá được vẽ trên 2 trục tọa độ được biểu diễn trên hình 11. S (m) là sức bền vật liệu ứng với chu kỳ 10³ và được xác định như sau:

Thông số S (e) được biểu thị ở chu kỳ 10^6, và 1 đường thẳng được vẽ giữa S (m) và S (e). Hàm của đường thẳng từ S (m) đến S (e) được Wöhler xác định như sau:

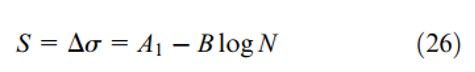
Khi S = S (a) là ứng suất luân phiên S_m được tính toán bằng cách sử dụng ứng suất tối đa và tối thiểu:

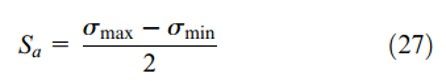
Độ bền mỏi được cho bởi số chu kỳ ứng với mọi ứng suất luân phiên S (a) ( hoặc σ (a)) có thể được tính toán theo hàm của Wöhler với 2 điều kiện biên sau :

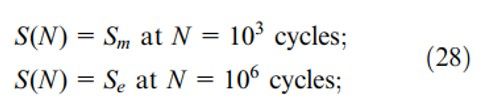
Bảng 6. Các yếu tố giảm sức bền mỏi

Bảng 7. Sức bền mỏi và tuổi thọ

B2bmart.vn vừa hướng dẫn bạn đọc về quy trình tính toán và thiết kế lo xo lá parabol. Đây là những kiến thức vô cùng hữu ích và giá trị. Hy vọng mọi người có thể hiểu và ứng dụng thật tốt vào công việc của mình.